オーバートーン測定は何故有効なのか？

QSenseのQCM-D測定においては、エネルギー散逸係数であるDの情報を用いるだけでなく、複数のオーバートーン（倍音）情報を取得することで、粘弾性を持つ材料の特性についてより深く複合的に理解することが可能になっております。この記事では、QSenseの取得するオーバートーンの情報を用いることで、お客様の研究においてどのような付加価値を提供しているのかについて実例を用いながらより詳しく見ていくことにします。

オーバートーンとは何か？　

ここでは、様々な厚さの理論的なポリマー層を前提にオーバートーンについて考察してみましょう。オーバートーン（倍音）は、サンプルとなる材料、特にポリマーの様な柔らかい材料について異なる視点を提供してくれます。

物理学の法則によれば、液体や軟らかい媒体物質内の音響せん断波δの浸透深さは、せん断振動の周波数が増えるにつれて減少していきます。

ここで、ηおよびρは媒体の粘度および密度であり、ωは角周波数となります。式１から導かれる直接の結果として、異なるオーバートーンは、センサ表面の上にある軟材料で構成される層に対してそれぞれ異なる応答をすることになります。光学測定法における異なる衝突角と波長の関係と同様に、異なるオーバートーン数は、対象材料の持つほんのわずかではあるがそれぞれ異なる遠近感に関する情報を示唆します。例えば図１のような3 次元の物体を観察しようとするとき、その外観の全体像を正確に把握するためには、様々な角度から観察を行う必要があるという事例をイメージして頂くと分かりやすいかもしれません。この場合、ある一つの角度からの観察から得た画像だけでは、観察者を欺き誤解を与える危険性があり、且つ不完全なものになってしまいます。

図1. 異なる角度から見た三次元の立体物の図

せん断振幅(shear amplitude)は、ハーモニクス（高調波）とセンサの負荷によって変動します。QCMに用いられているピエゾ振動子にはその固有の特性により、センサ表面の振動・振幅がオーバートーン数の増加に伴い減少するという特徴があります。センサ負荷が増加すると（この例では膜厚が増加することで）、Δf、ΔDがそれぞれ減少するのと同様に振幅は減少していきます。

ある膜厚においては、最大せん断振幅の値が下落する現象(dip)を観測することができます(図2）。この現象が起きるとき、膜厚は放出せん断波と反射せん断波の間の最大逆位相の位置に相当するため、従ってオーバートーン数の違いに伴い変動することになります。

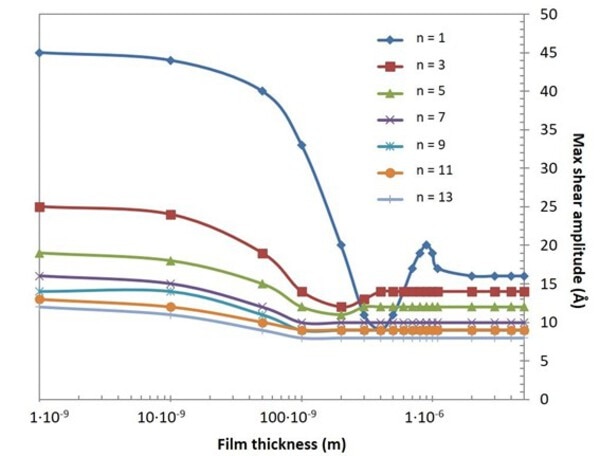
図2 ハーモニクス（高調波）n=1, 3, 5, 7, 9, 11, 13について、センサ表面での最大せん断振動での振幅値を膜厚の関数としてモデル化したもの。このプロットは、センサ表面の最大振動振幅がオーバートーン数の増加とともに減少することを示しています。また、ある膜厚では、振幅に下落（dip）があることを示しています。このdipは、放出せん断波と反射せん断波の最大の逆位相に相当します。

この現象は、膜厚を変えて膜全体でのせん断波の振動振幅を考えてみると、図３のように明らかになります。

- 1nmの場合 ：厚みが1nmの膜は基本的に剛性が高く、せん断波の浸透深さであるδよりもはるかに薄いため、膜中における変位はほぼ一定となります（図3A-B）。

- 10 nmの場合：10 nmの膜の場合、質量負荷の増加によって振幅が小さくなる点を除けば全体的な挙動は1nmの膜と非常によく似ています、図3A-Bを参照下さい。

- 150 nmの場合：膜厚を 150 nm まで厚くすると、せん断波の反射と重畳現象が明確になり、センサ面から伝搬させた時に変位が大きくなることがわかります（図 3A,3C）。すなわちソフトな膜を通過した際に起きるダンピング効果により、薄膜や硬い膜に比べてセンサ表面での変位はかなり小さくなる現象が起きていることを示しています。

- 300nmの場合：厚さを300nmまで増加させると、減衰効果はより顕著になります。放出せん断波と反射せん断波の間の重畳によってもたらされる効果もまた、振幅が最初に減少し、その後増加するので、より明確になります（”destructive respective constructive superposition”と呼ばれる現象） 

- 1μmの場合：厚さが1μmの膜では、図3Aのように、振動振幅は顕著な減少傾向を示し、最後にせん断波の反射効果によってほんのわずかに増加します。

- 5μmの場合：図3Aにある通り、5μmの膜厚の場合、せん断波は上部界面に到達する前に完全に消滅し、反射も起こらず、重畳現象は発生しません。

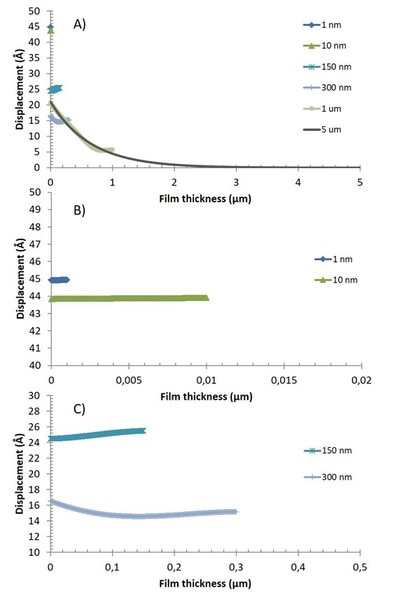
図3. 厚さ1nm、10nm、150nm、300nm、1μm、5μmの様々な膜厚の膜全体における、基本周波数に対するせん断波の振動振幅をモデル化した図。A）はすべての膜厚におけるせん断波の振動振幅の様子を示し、B)は、1 nm と 10 nm の膜の挙動を明らかにするため、A)の該当部分のみ拡大した。C）についても、150 nm と 300 nm の膜の挙動を明らかにするため、A）の該当部分をやはり拡大したものである。

前述したように、オーバートーン数が増加すると、振幅の消衰深度とともに変位量も小さくなる（図2参照）。しかし、基本周波数における一般的な挙動については、図 3に示されているものと等しくなる。

オーバートーンにおけるfとDの応答は膜の特性に依存する

一般的に共振が小さくなると、感知する質量については相対的に大きくなるため、ΔfとΔDの反応については横方向に均質な膜の場合大きくなる傾向があります。(図4)。

既述の通り、共振の空間方向の浸透深さδと波長は、共に周波数が高くなるにつれて減少していきます。その結果、重畳効果がシフトし、周波数とエネルギー散逸のピーク（最大逆位相）はより早く、つまり膜厚が比較的小さい場合に、オーバートーン数が増加した状態で発生することになります。

硬い膜（rigid film）の場合、すなわち、ここで与えられた例ではΔfとΔDが低い場合にっついては、粘弾性の応答は無視できるほど小さくなるため、すべてのオーバートーンのfとDの曲線は重なります（図4）。しかし、膜が柔らかくソフトになると（この図でいえば膜厚が増すと）、浸透深さや波長の違いにより、オーバートーンは明確に分離します。

膜厚がδを超えて厚くなると、ΔfとΔDの応答は最終的に一定の値に収束します。この状態になると、膜の表面に形成されたいかなる付加膜に関する情報も感知することができなくなり、ΔfおよびΔDは変動しなくなります。

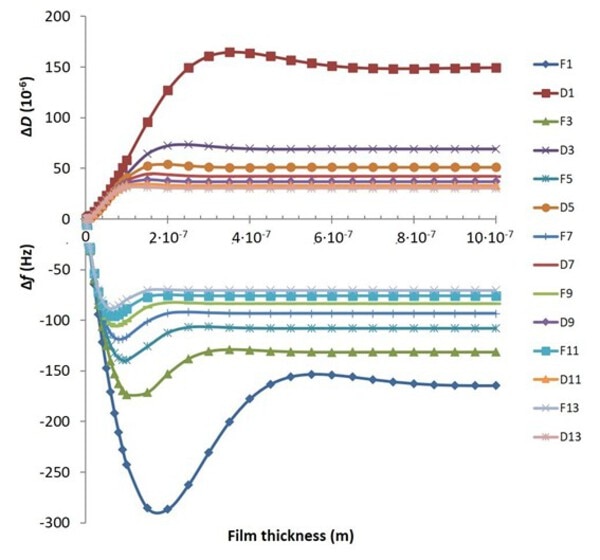
図4：異なるオーバートーンにおけるΔfとΔDの応答の様子（対膜厚の関数として）。膜厚が薄い場合、すべてのオーバートーンが重なっていることから、膜の粘弾性から受ける応答はほんのわずかであり、fとDの曲線に影響を与えないことを示しています。しかし膜厚が増加すると、オーバートーンは分離を始めることがわかります。

粘弾性応答の違い~D vs fの図から読み解く

ここでエネルギー散逸のシフトであるΔDを周波数シフトであるΔfの関数としてプロットすると、異なるオーバートーンについて粘弾性応答の違いが明らかになります（図5）。この図からソフト膜中のせん断波の反射と重畳効果に起因してΔDとΔfの対応関係がらせん状の曲線になることがわかり、またΔDの値が特定の値になると、同時に2つ、3つ、あるいは4つといった複数の異なるΔfの値に対応するという事実が浮かび上がります。

このらせん状の曲線におけるΔfの挙動からは、一般的に質量負荷が増加した場合に硬い膜から予想されるΔfの減少挙動ではなく、Δfの増加挙動を観測する可能性も導かれます。従ってソフトな膜の特性を決定するためには、質量や厚さといった情報だけでなく、粘性や弾性率といった情報も必要とすることになります。これらの事実から1つのオーバートーン（すなわち、2つの入力パラメータΔfとΔD）だけを用いると、QCMを応用した測定システムにおける粘弾性特性を決定するための十分な情報を得ることができないことがわかります。従ってQCMの測定システムから得られた情報を完全に理解するために必要不可欠な補完情報を提供するという役割を考えると、複数の異なるオーバートーンによる測定には非常に重要な意味があるのです。

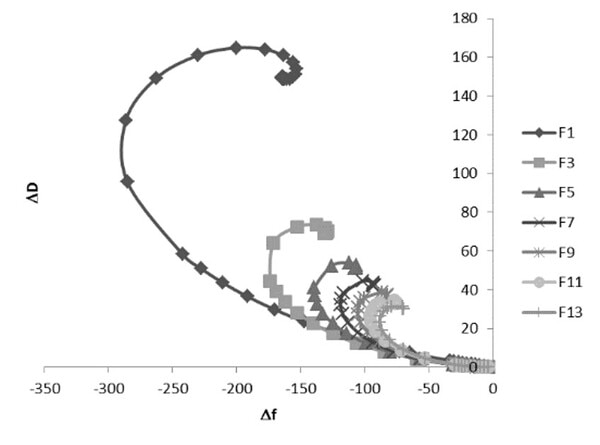
図5. 異なるオーバートーンでの周波数シフトΔfの関数としてプロットしたエネルギー散逸シフトΔD。ΔDのある特定の値が、2つ、3つ、あるいは4つといった異なる複数のΔfの値に相当していることが明らかになる。

まとめ

これまで述べてきた様に、QCMの共振の振幅と重畳効果は、ΔfとΔDと同様、異なるオーバートーンではそれぞれ異なる応答を示します。このことから、オーバートーン測定はセンサ表面上の試料材料が持つ特性を推定するために必要な事実や情報を異なる視点から提供してくれるという点で、大変有意義で役立つものであることを改めてご理解頂けたものと思います。(図1の3次元立体図を用いた例えを思い出して頂ければ幸いです)。これを数学的に表現するならば、粘弾性のモデル式を用いてより正確なソフト膜の材料特性（ここでは質量/膜厚と粘性および弾性）の値を推定し算出するためには、より多くの入力パラメータを持っておくことが重要であると言い換えることもできます。